Esta guia es creada con el fin de tener una referencia donde consultar sobre Tensorflow, es una recopilacion de otras paginas web y blogs las cuales menciono al final de esta guia y agradesco enormemente.
Tensor flow es una biblioteca desarrollada por Google que nos permite realizar Machine Learning, con esta biblioteca podemos crear redes neuronales utilizando grafos.
Es un conjunto de objetos llamados vértices o nodos unidos por enlaces llamados aristas o arcos, que permiten representar relaciones binarias entre elementos de un conjunto.
Una red neuronal es un grafo dirigido construido a partir de elementos computacionales basicos. Una red neuronal codifica funciones numericas.
Son un enfoque computacional, que se basa en una gran colección de unidades neurales (también conocido como neuronas artificiales), para modelar libremente la forma en que un cerebro biológico resuelve problemas con grandes grupos de neuronas biológicas conectados por los axones. Cada unidad neuronal está conectada con otras, y los enlaces se pueden aplicar en su efecto sobre el estado de activación de unidades neuronales conectadas. Cada individuo de la unidad neuronal puede tener una función de suma, que combina conjuntamente los valores de todas las entradas. Puede haber una función umbral o función de limitación en cada conexión y en la propia unidad: de tal manera que la señal debe superar el límite antes de la propagación a otras neuronas.
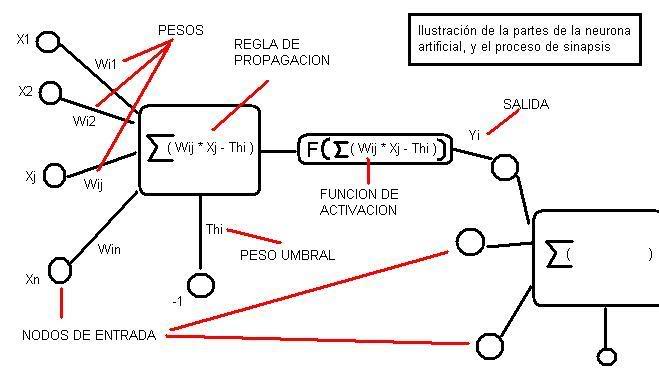
La unidad básica de una RNA es la neurona. Aunque hay varios tipos de neuronas diferentes, la mas comun es la de tipo McCulloch-Pitts. En la siguiente figura puede verse una representación de la misma.
Una neurona artificial es un procesador elemental, en el sentido de que procesa un vector x (x1,x2,...xN) de entradas y produce un respuesta o salida única. Los elementos clave de una neurona artificial los podemos ver en la figura anterior y son los siguientes:
-
Las entradas que reciben los datos de otras neuronas. En una neurona biológica corresponderían a las dendritas
-
Los pesos sinapticos wij. Al igual que en una neurona biológica se establecen sinápsis entre las dendritas de una neurona y el axón de otra, en una neurona artificial a las entradas que vienen de otras neuronas se les asigna un peso, un factor de importancia. Este peso, que es un número, se modifica durante el entrenamiento de la red neuronal, y es aquí por tanto donde se almacena la infomación que hara que la red sirva para un propósito u otro.
-
Una regla de propagación. Con esas entradas y los pesos sinapticos, se suele hacer algun tipo de operación para obtener el valor del potencial postsinaptico (valor que es funcion de las entradas y los pesos y que es el que se utiliza en último término para realizar el procesamiento). Una de las operaciones mas comunes es sumar las entradas, pero teniendo en cuenta la importancia de cada una (el peso sináptico asociado a cada entrada). Es lo que se llama suma ponderada, aunque otras operaciones también son posibles.
-
Una función de activación. El valor obtenido con la regla de propagación, se filtra a través de una función conocida como función de activación y es la que nos da la salida de la neurona. Según para lo que se desee entrenar la red neuronal, se suele escoger una función de activación u otra en ciertas neuronas de la red. En la siguiente tabla se muestran las funciones de activación mas usuales.
En muchas ocasiones la razón para la aplicación de una función de activación distinta de la identidad surge de la necesidad de que las neuronas produzcan una salida acotada. Esto desde un punto de vista de similitud con el sistema biológico, no es tan descabellado, ya que las respuestas de las neuronas biológicas estan acotadas en amplitud. Además cada neurona tiene asociado un número denominado bías o umbral, que puede verse como un número que indica a partir de que valor del potencial postsináptico la neurona produce una salida significativa.
Desde un punto de vista matemático, se puede ver una red neuronal como un grafo dirigido y ponderado donde cada uno de los nodos son neuronas artificiales y los arcos que unen los nodos son las conexiones sinápticas. Al ser dirigido, los arcos son unidireccionales. ¿Que quiere decir esto? En el lenguaje de neuronas y conexiones significa que la información se propaga en un unico sentido, desde una neurona presinaptica (neurona origen) a una neurona postsináptica (neurona destino)
Por otra parte es ponderado, lo que significa que las conexiones tienen asociado un número real, un peso, que indica la importancia de esa conexión con respecto al resto de las conexiones. Si dicho peso es positivo la conexión se dice que es excitadora, mientras que si es negativa se dice que es inhibidora.
Lo usual es que las neuronas se agrupen en capas de manera que una RNA esta formada por varias capas de neuronas. Aunque todas las capas son conjuntos de neuronas, según la funcion que desempeñan, suelen recibir un nombre especifico. Las mas comunes son las siguientes:
-
Capa de entrada: las neuronas de la capa de entrada, reciben los datos que se proporcionan a la RNA para que los procese.
-
Capas ocultas: estas capas introducen grados de libertad adicionales en la RNA. El número de ellas puede depender del tipo de red que estemos considerando. Este tipo de capas realiza gran parte del procesamiento.
-
Capa de salida: Esta capa proporciona la respuesta de la red neuronal. Normalmente también realiza parte del procesamiento.
Según el criterio que escojamos para clasificar las RNA tendremos una clasificacion u otra. Lo más común es usar la arquitectura y el tipo de aprendizaje como criterios de clasificación.
Si nos fijamos en la arquitectura podemos tener dos posibilidades distintas. Si la arquitectura de la red no presenta ciclos, es decir, no se puede trazar un camino de una neurona a sí misma, la red se llama unidireccional (feedforward).
Por el contrario, si podemos trazar un camino de una neurona a sí misma la arquitectura presenta ciclos. Este tipo de redes se denominan recurrentes o realimentados (recurrent).
-
El otro criterio mas habitual para clasificar las redes neuronales es el tipo de aprendizaje que se utilice. Hay cuatro clases de aprendizaje distintos:
-
Aprendizaje supervisado: En este tipo de aprendizaje se le proporciona a la RNA una serie de ejemplos consistentes en unos patrones de entrada, junto con la salida que debería dar la red. El proceso de entrenamiento consiste en el ajuste de los pesos para que la salida de la red sea lo más parecida posible a la salida desada. Es por ello que en cada iteración se use alguna función que nos de cuenta del error o el grado de acierto que esta cometiendo la red. Existen dos tipos de aprendizaje supervisado:
-
Sistemas de Regresión de Aprendizaje de Máquina: Sistemas donde el valor que se predice está en algún lugar de un espectro continuo. Estos sistemas nos ayudan con preguntas tipo “¿Cuánto es?” o “¿Cuántos son?”.
-
Sistemas de Clasificación de Aprendizaje de Máquina: Sistemas en los cuales se busca una predicción de sí-o-no, por ejemplo: “¿Este tumor es cancerígeno?”, “¿Esta galleta pasó nuestro estándar de calidad?” y preguntas por el estilo.
-
-
Aprendizaje no supervisado o autoorganizado: En este tipo de aprendizaje se presenta a la red una serie de ejemplos pero no se presenta la respuesta deseada. Lo que hace la RNA es reconocer regularidades en el conjunto de entradas, es decir, estimar una funcion densidad de probabilidad p(x) que describe la distribucion de patrones x en el espacio de entrada Rn .
-
Aprendizaje Híbrido: Es una mezcla de los anteriores. Unas capas de la red tienen un aprendizaje supervisado y otras capas de la red tienen un aprendizaje de tipo no supervisado. Este tipo de entrenamiento es el que tienen redes como las RBF.
-
Aprendizaje reforzado (reinforcement learning): Es un aprendizaje con caracteristicas del supervisado y con caracteristicas del autoorganizado. No se proporciona una salida deseada, pero si que se le indica a la red en cierta medida el error que comete, aunque es un error global.
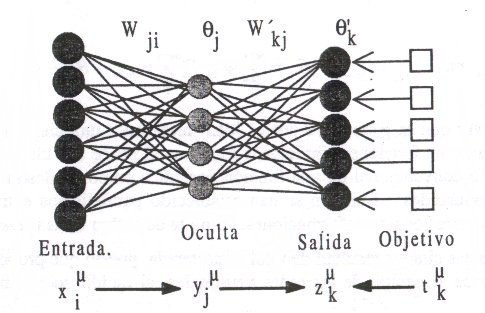
Este es uno de los tipos de redes más comunes. Se basa en otra red mas simple llamada perceptrón simple solo que el número de capas ocultas puede ser mayor o igual que una. Es una red unidireccional (feedforward). La arquitectura típica de esta red es la siguiente:
Las neuronas de la capa oculta usan como regla de propagación la suma ponderada de las entradas con los pesos sinápticos wij y sobre esa suma ponderada se aplica una función de transferencia de tipo sigmoide, que es acotada en respuesta.
El aprendizaje que se suele usar en este tipo de redes recibe el nombre de retropropagacion del error (backpropagation). Como funcion de coste global, se usa el error cuadratico medio. Es decir, que dado un par (xk, dk) correspondiente a la entrada k de los datos de entrenamiento y salida deseada asociada se calcula la cantidad:
que vemos que es la suma de los errores parciales debido a cada patrón (índice p), resultantes de la diferencia entre la salida deseada dp y la salida que da la red f(.) ante el vector de entrada xk. Si estas salidas son muy diferentes de las salidas deseadas, el error cuadratico medio sera grande. f es la función de activación de las neuronas de la capa de salida e y la salida que proporcionan las neuronas de la ultima capa oculta.
-
Inicializar los pesos y los umbrales iniciales de cada neurona. Hay varias posibilidades de inicialización siendo las mas comunes las que introducen valores aleatorios pequeños.
-
Para cada patrón del conjunto de los datos de entrenamiento
-
Obtener la respuesta de la red ante ese patrón. Esta parte se consigue propagando la entrada hacia adelante, ya que este tipo de red es feedforward. Las salidas de una capa sirven como entrada a las neuronas de la capa siguiente, procesandolas de acuerdo a la regla de propagación y la función de activación correspondientes.
-
Calcular los errores asociados según la ecuación 3-2
-
Calcular los incrementos parciales (sumandos de los sumatorios). Estos incrementos dependen de los errores calculados en 2.b
-
Calcular el incremento total ,para todos los patrones, de los pesos y los umbrales según las expresiones en la ecuación 3-2
-
Actualizar pesos y umbrales
-
Calcular el error actual y volver al paso 2 si no es satisfactorio.
TensorFlow es un sistema de programación en el que representamos cálculos en forma de grafos. Los nodos en el grafo se llaman ops (abreviatura de operaciones). Una op tiene cero o más tensores, realiza algún cálculo, y produce cero o más tensores.
Un grafo de TensorFlow es una descripción de cálculos. Para calcular cualquier cosa dentro de TensorFlow, el grafo debe ser lanzado dentro de una sesión. La Sesión coloca las operaciones del grafo en los diferentes dispositivos, tales como CPU o GPU, y proporciona métodos para ejecutarlas.
Los programas TensorFlow utilizan una estructura de datos llamada tensor para representar todos los datos. Puede pensar en un tensor como una matriz o lista n-dimensional. Un tensor tiene un tipo estático y dimensiones dinámicas. Sólo se pueden pasar tensores entre nodos en el grafo de cálculo.
Podemos construir ops de constantes utilizando constant, su API es bastante simple:
constant(value, dtype=None, shape=None, name='Const', verify_shape=False)Argumentos:
- value: Un valor constante (o lista) del tipo de salida dtype.
- dtype: El tipo de los elementos del tensor resultante.
- shape: Dimensiones opcionales del tensor resultante.
- name: Nombre opcional para el tensor.
- verify_shape: Boolean que permite verificar una forma (shape) de valores.
Retorna: Un tensor constante
Le debemos pasar un valor, el cual puede ser cualquier tipo de tensor (un escalar, un vector, una matriz, etc) y luego opcionalmente le podemos pasar el tipo de datos, la forma y un nombre.
# Creación de Constantes
# El valor que retorna el constructor es el valor de la constante.
# creamos constantes a=2 y b=3
a = tf.constant(2)
b = tf.constant(3)
# creamos matrices de 3x3
matriz1 = tf.constant([[1, 3, 2],
[1, 0, 0],
[1, 2, 2]])
matriz2 = tf.constant([[1, 0, 5],
[7, 5, 0],
[2, 1, 1]])
# Realizamos algunos cálculos con estas constantes
suma = tf.add(a, b)
mult = tf.mul(a, b)
cubo_a = a**3
# suma de matrices
suma_mat = tf.add(matriz1, matriz2)
# producto de matrices
mult_mat = tf.matmul(matriz1, matriz2)tf.add(x, y, name=None)Devuelve x + y por elemento. Argumentos:
- x: Un Tensor. Debe ser uno de los siguientes tipos: half, float32, float64, uint8, int8, int16, int32, int64, complex64, complex128, string.
- y: Un Tensor. Debe tener el mismo tipo que x.
- name: Un nombre para la operación (opcional).
Retorna: Un Tensor. Tiene el mismo tipo que x.
tf.matmul(a, b, transpose_a=False, transpose_b=False, adjoint_a=False, adjoint_b=False, a_is_sparse=False, b_is_sparse=False, name=None)Multiplica la matriz a por la matriz b, produciendo a * b. Ejemplos:
# 2-D tensor `a`
a = tf.constant([1, 2, 3, 4, 5, 6], shape=[2, 3]) => [[1. 2. 3.]
[4. 5. 6.]]
# 2-D tensor `b`
b = tf.constant([7, 8, 9, 10, 11, 12], shape=[3, 2]) => [[7. 8.]
[9. 10.]
[11. 12.]]
c = tf.matmul(a, b) => [[58 64]
[139 154]]
# 3-D tensor `a`
a = tf.constant(np.arange(1, 13, dtype=np.int32),
shape=[2, 2, 3]) => [[[ 1. 2. 3.]
[ 4. 5. 6.]],
[[ 7. 8. 9.]
[10. 11. 12.]]]
# 3-D tensor `b`
b = tf.constant(np.arange(13, 25, dtype=np.int32),
shape=[2, 3, 2]) => [[[13. 14.]
[15. 16.]
[17. 18.]],
[[19. 20.]
[21. 22.]
[23. 24.]]]
c = tf.matmul(a, b) => [[[ 94 100]
[229 244]],
[[508 532]
[697 730]]]Argumentos:
- a: Tensor de tipo float16, float32, float64, int32, complex64, complex128 and rank > 1.
- b: Tensor con el mismo tipo y rango que a.
- transpose_a: Si es cierto, a se transpone antes de la multiplicación.
- transpose_b: Si es cierto, b se transpone antes de la multiplicación.
- adjoint_a: Si es cierto, a se conjuga y se transpone antes de la multiplicación.
- adjoint_b: Si es cierto, b se conjuga y se transpone antes de la multiplicación.
- a_is_sparse: Si es cierto, a se trata como una matriz dispersa.
- b_is_sparse: Si es cierto, b se trata como una matriz dispersa.
- name: Nombre de la operación (opcional).
Retorna: Un Tensor del mismo tipo que a y b en el que cada matriz más interna es el producto de las matrices correspondientes en y b, ejem. Si todos los atributos de transposición o adjunto son False:
output[..., i, j] = sum_k (a[..., i, k] * b[..., k, j]), para todos los indices i, j.- Note: This is matrix product, not element-wise product.
Lanza:
- ValueError: Si transpose_a y adjoint_a, o transpose_b y adjunto_b están ambos en True.
tf.reduce_sum(input_tensor, axis=None, keep_dims=False, name=None, reduction_indices=None)Calcula la suma de elementos a través de las dimensiones de un tensor.
Reduce input_tensor a lo largo de las dimensiones dadas en el eje. A menos que keep_dims sea verdadero, el rango del tensor se reduce en 1 para cada entrada en el eje. Si keep_dims es verdadero, las dimensiones reducidas se conservan con longitud 1.
Si el eje no tiene entradas, todas las dimensiones se reducen y se devuelve un tensor con un solo elemento.
Ejemplo:
# 'x' is [[1, 1, 1]
# [1, 1, 1]]
tf.reduce_sum(x) ==> 6
tf.reduce_sum(x, 0) ==> [2, 2, 2]
tf.reduce_sum(x, 1) ==> [3, 3]
tf.reduce_sum(x, 1, keep_dims=True) ==> [[3], [3]]
tf.reduce_sum(x, [0, 1]) ==> 6Argumentos:
- input_tensor: El tensor para reducir. Debe tener tipo numérico.
- axis: Las dimensiones a reducir. Si es None (el valor predeterminado), reduce todas las dimensiones.
- keep_dims: If true, retains reduced dimensions with length 1.
- name: Si es verdadero, conserva dimensiones reducidas con longitud 1.
- reduction_indices: El nombre antiguo (obsoleto) para el eje.
Retorna: El tensor reducido.
tf.argmax(input, axis=None, name=None, dimension=None)Devuelve el índice con el mayor valor a través de los ejes de un tensor.
Argumentos:
- input: Un Tensor. Debe ser uno de los siguientes tipos: float32, float64, int64, int32, uint8, uint16, int16, int8, complex64, complex128, qint8, quint8, qint32, half.
- axis: Un Tensor. Debe ser uno de los siguientes tipos: int32, int64. int32, 0 <= axis < rank(input). Describe el eje del Tensor de entrada para reducir a través. Para vectores, utilice axis = 0.
- name: Un nombre para la operación (opcional).
Retorna: Un Tensor del tipo int64.
tf.equal(x, y, name=None)Evalua si es verdadero (x == y)
Argumentos:
- x: Un Tensor. Debe ser uno de los siguientes tipos: half, float32, float64, uint8, int8, int16, int32, int64, complex64, quint8, qint8, qint32, string, bool, complex128.
- y: Un Tensor. Debe tener el mismo tipo que x.
- name: Un nombre para la operación (opcional).
Retorna: A Tensor de tipo bool.
tf.cast(x, dtype, name=None)Emite un tensor a un nuevo tipo.
La operación ejecuta x (en caso de Tensor) o x.values (en caso de SparseTensor) para dtype.
Por Ejemplo:
# tensor `a` is [1.8, 2.2], dtype=tf.float
tf.cast(a, tf.int32) ==> [1, 2] # dtype=tf.int32Argumentos:
- x: Un Tensor o Tensor Disparo.
- dtype: El tipo de destino.
- name: Un nombre para la operación (opcional).
Retorna: Un Tensor o SparseTensor con la misma forma que x.
Ahora que ya definimos algunas ops constantes y algunos cálculos con ellas, debemos lanzar el grafo dentro de una Sesión. Para realizar esto utilizamos el objeto Session. Este objeto va a encapsular el ambiente en el que las operaciones que definimos en el grafo van a ser ejecutadas y los tensores son evaluados.
# Todo en TensorFlow ocurre dentro de una Sesión
# creamos la sesion y realizamos algunas operaciones con las constantes
# y lanzamos la sesión
with tf.Session() as sess:
print("Suma de las constantes: {}".format(sess.run(suma)))
print("Multiplicación de las constantes: {}".format(sess.run(mult)))
print("Constante elevada al cubo: {}".format(sess.run(cubo_a)))
print("Suma de matrices: \n{}".format(sess.run(suma_mat)))
print("Producto de matrices: \n{}".format(sess.run(mult_mat)))Las Sesiones deben ser cerradas para liberar los recursos, por lo que es una buena práctica incluir la Sesión dentro de un bloque "with" que la cierra automáticamente cuando el bloque termina de ejecutar.
Para ejecutar las operaciones y evaluar los tensores utilizamos Session.run().
Las Variables mantienen el estado a través de las ejecuciones del grafo. Son buffers en memoria que contienen tensores. Se deben inicializar explícitamente y se pueden guardar en el disco para luego restaurar su estado de necesitarlo. Se crean utilizando el objeto Variable.
# Creamos una variable y la inicializamos con 0
estado = tf.Variable(0, name="contador")
# Creamos la op que le va a sumar uno a la Variable `estado`.
uno = tf.constant(1)
nuevo_valor = tf.add(estado, uno)
actualizar = tf.assign(estado, nuevo_valor)
# Las Variables deben ser inicializadas por la operación `init` luego de
# lanzar el grafo. Debemos agregar la op `init` a nuestro grafo.
init = tf.initialize_all_variables()
# Lanzamos la sesion y ejecutamos las operaciones
with tf.Session() as sess:
# Ejecutamos la op `init`
sess.run(init)
# imprimir el valor de la Variable estado.
print(sess.run(estado))
# ejecutamos la op que va a actualizar a `estado`.
for _ in range(3):
sess.run(actualizar)
print(sess.run(estado))Las Variables simbólicas o Contenedores nos van a permitir alimentar a las operaciones con los datos durante la ejecución del grafo. Estos contenedores deben ser alimentados antes de ser evaluados en la sesión, sino obtendremos un error.
# Ejemplo variables simbólicas en los grafos
# El valor que devuelve el constructor representa la salida de la
# variable (la entrada de la variable se define en la sesion)
# Creamos un contenedor del tipo float. Un tensor de 4x4.
x = tf.placeholder(tf.float32, shape=(4, 4))
y = tf.matmul(x, x)
with tf.Session() as sess:
# print(sess.run(y)) # ERROR: va a fallar porque no alimentamos a x.
rand_array = np.random.rand(4, 4)
print(sess.run(y, feed_dict={x: rand_array})) # ahora esta correcto.import csv
import tensorflow as tf
import random
import pandas as pd
import numpy as np
# Uamos panda para leer el archivo csv
ipd = pd.read_csv("iris.csv")
# Tomamos las especies, las transformamos en una matriz con 3 columnas, correspondientes a cada tipo con valor booleano
# y la insertamos en la columna One-hot
species = list(ipd['Species'].unique())
ipd['One-hot'] = ipd['Species'].map(lambda x: np.eye(len(species))[species.index(x)] )
# Desordenamos las muestras, y dejamos 100 para entrenamiento y 50 para test
shuffled = ipd.sample(frac=1)
trainingSet = shuffled[0:len(shuffled)-50]
testSet = shuffled[len(shuffled)-50:]
# Definimos el feed de muestra, los pesos y las bias
inp = tf.placeholder(tf.float32, [None, 4])
weights = tf.Variable(tf.zeros([4, 3]))
bias = tf.Variable(tf.zeros([3]))
# Realizamos la activacion con softmax
y = tf.nn.softmax(tf.matmul(inp, weights) + bias)
# Definimos el feed con los resultados esperados
y_ = tf.placeholder(tf.float32, [None, 3])
# Calculamos la entropia cruzada
cross_entropy = -tf.reduce_sum(y_*tf.log(y))
# Entrenamos la red utilizando el algoritmo de optimizacion de gradiente descendente
# llamado Adaptive Moment Estimation (Adam)
train_step = tf.train.AdamOptimizer(0.01).minimize(cross_entropy)
# Define si es una prediccion correcta evaluando si la posicion del valor mas
# grande de la muestra, es el mismo que el calculado
correct_prediction = tf.equal(tf.argmax(y,1), tf.argmax(y_,1))
# Precision
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
init = tf.initialize_all_variables()
sess = tf.Session()
sess.run(init)
keys = ['Sepal Length', 'Sepal Width','Petal Length', 'Petal Width']
# Iteramos el entrenamiento 1000 veces
for i in range(1000):
train = trainingSet.sample(50)
sess.run(train_step, feed_dict={inp: [x for x in train[keys].values],
y_: [x for x in train['One-hot'].as_matrix()]})
print sess.run(accuracy, feed_dict={inp: [x for x in testSet[keys].values],
y_: [x for x in testSet['One-hot'].values]})
# Creamos un metodo predictivo
def classify(inpv):
dim = y.get_shape().as_list()[1]
res = np.zeros(dim)
largest = sess.run(tf.argmax(y,1), feed_dict={inp: inpv})[0]
return np.eye(dim)[largest]
# Tomamos una muestra y testeamos
sample = shuffled.sample(1)
print "Classified as %s" % classify(sample[keys])from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import tensorflow as tf
import numpy as np
# Data sets
IRIS_TRAINING = "iris_training.csv"
IRIS_TEST = "iris_test.csv"
# Se cargan los datasets, de entrenamiento y de testeo
training_set = tf.contrib.learn.datasets.base.load_csv_without_header(
filename=IRIS_TRAINING, # Path del archivo csv
target_dtype=np.int, # Tipo de dato de los objetivos especificado con Numpy
features_dtype=np.float32) # Tipo de dato de las caracteristicas
# especificado con Numpy
test_set = tf.contrib.learn.datasets.base.load_csv_without_header(
filename=IRIS_TEST,
target_dtype=np.int,
features_dtype=np.float32)
# tf.contrib.layers.real_valued_column Define las columnas que representan
# las caracteristicas a analizar. El primer parametro es el nombre
# el segundo especifica la dimencion que debe contener las columnas de
# entrada, en este caso las 4 primeras
feature_columns = [tf.contrib.layers.real_valued_column("", dimension=4)]
# Construir 3 capas DNN con 10, 20, 10 unidades respectivamente.
# DNN es Deep Neural Network Classifier, feature_columns son las columnas de
# entrada, lo que se conoce como los input, hidden_units es un array que
# representa las capas ocultas indicando cuantas neuronas tiene por capas
# en el ejemplo de abajo son 3 capas ocultas con 10, 20 y 10 neuronas cada
# una respectivamente y n_classes representa las clases de salidas en que
# representara la neurona de salida, model_dir es donde tensorflow guarda
# los checkpoints
classifier = tf.contrib.learn.DNNClassifier(feature_columns=feature_columns,
hidden_units=[10, 20, 10],
n_classes=3,
model_dir="/tmp/iris_model")
# Ajustar el modelo (fit=ajustar).
classifier.fit(x=training_set.data, # Caracteristicas de entrenamiento
y=training_set.target, # Valor objetivo real de entrenamiento
steps=2000)
# Evaluar la exactitud (accuracy=exactitud)
accuracy_score = classifier.evaluate(x=test_set.data, # Caracteristicas de prueba
y=test_set.target)["accuracy"] # Valor objetivo real de prueba
print('Accuracy: {0:f}'.format(accuracy_score))
# Clasificar dos flores de ejemplo
new_samples = np.array(
[[6.4, 3.2, 4.5, 1.5], [5.8, 3.1, 5.0, 1.7]], dtype=float)
# classifier.predict predice segun el entrenamiento anterior y las pruebas
y = list(classifier.predict(new_samples, as_iterable=True))
print('Predictions: {}'.format(str(y)))Los ejemplos anteriormente mencionados estan en este repositorio con los dataset correspondientes.