Merkle Tree in PHP

This README.md file describes a PHP implementation of Ralph Merkle's hash tree, also called "The Merkle Tree". The Merkle tree is essentially a binary tree, where nodes can have one or two children (not zero, as that would be a leaf). Once the algorithm is finished, on top of the Merkle tree we will find a hash value called "Merkle Root", which is a unique value representing all the leaves.

In this implementation I only want to obtain the Merkle root, the value on top of the Merkle tree.

How it works

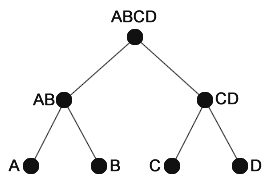
The Merkle tree algorithm starts with a set of data, which can be a simple string, or a file, or ... The only condition is that it must be "hashable". Let's suggest four data blocks called A, B, C and D.

The first thing to do is to convert those blocks into a hash value. In the algorithm this is done by adding them to the tree (see method Add).

When the values are placed as leaves of the Merkle tree it is time to create parents, who's value is the hash of its children's hashes. Let's see a small example.

A is the hashed value for the first data, B for the second, and so on. AB is the hashed value of both A and B hashes put together. And ABCD is the hashed value for AB and CD put together. So, the Merkle root for values A, B, C and D is ABCD.

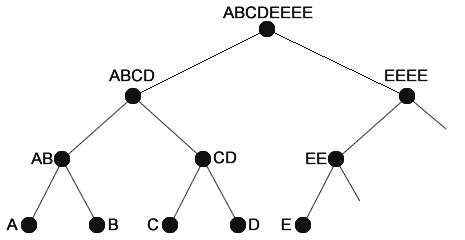
This is an ideal path. But what happens if we have a number different than a power of two? In this case we'll have to duplicate the odd values. Let's see how with one more data origin (A, B, C, D and E):

This will require a bit more of explanation. Let's enumerate the steps of the algorithm:

1. A and B are hashed to obtain AB
2. C and D are hashed to obtain CD
3. E has no right sibling, so we duplicate the item and create EE We go one level up!
4. AB and CD are hashed to obtain ABCD
5. EE has no right sibling, so we duplicate the item and create EEEE We go one level up!
6. ABCD and his right sibling EEEE are hashed together to obtain ABCDEEEE, which is finally the Merkle Root

This method covers all possible number of data sets. We can always generate a Merkle root with this algorithm.

Uses

The Merkle Root is widely used in blockchain and cryptocurrency, but can also be used in file transfer or file check.

Proof-of-Inclusion

Although this topic is not covered in this implementation, the Proof-of-Inclusion is one of the important aspects of the Merkle tree. Lets imagine we have a thousand of signatures to hash, and that we have already a Merkle root for all those signatures.

For one given signature, can we easily proof its inclusion in the Merkle Root? Without the Merkle root you would need access to all the signatures in order to recreate all the hashes and check the hashed value.

With a Merkle tree this becomes very much elegant and fast. You only need access to the element itself, the Merkle root, and the hashes of all the siblings. Difficult to understand? Have a look at the following gif:

Wonderful gif by Nakamoto.com.

The cost of the Proof-of-Inclusion is always O(log n), which is an amazing performance improvement.

Implementation decisions

• I don't provide a Proof-of-Inclusion method.
• The add method hashes the added element, so the leaves are already there when starting the algorithm.

Installation

First, clone this repository:

$ git clone https://github.com/oscarpascualbakker/merkle-tree.git .

Then, run the commands to build and run the Docker image:

$ docker build -t merkle .
$ docker container run --rm -v $(pwd):/var/www/html/ merkle php merkle.php

(use %cd% on Windows, or ${PWD} on Mac)

Tests can be run this way:

$ docker container run -it --rm merkle vendor/bin/phpunit ./tests

Further readings

If you are interested in Merkle Trees, don't miss the opportunity to visit the following pages:

• https://www.derpturkey.com/merkle-tree-construction-and-proof-of-inclusion/
• https://medium.com/coinmonks/merkle-trees-concepts-and-use-cases-5da873702318
• https://nakamoto.com/merkle-trees/

Comments

I am preparing a cryptocurrency, and I needed a Merkle root for the transactions. Although PHP is not the best language for a cryptocurrency, a Merkle Tree can be useful for other purposes, so I decided to upload it to my github account. I hope you can use it in your projects.

As usual, don't hesitate to give me your feedback. I'm glad to improve this algorithm with your help.

And if you like this code, why don't you buy me a coffee? :-)

Cheers!