forked from javadev/LeetCode-in-Java
-
Notifications
You must be signed in to change notification settings - Fork 0
Commit
This commit does not belong to any branch on this repository, and may belong to a fork outside of the repository.
- Loading branch information
Showing
15 changed files
with
491 additions
and
0 deletions.
There are no files selected for viewing
48 changes: 48 additions & 0 deletions
48
src/main/java/g3001_3100/s3020_find_the_maximum_number_of_elements_in_subset/Solution.java
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,48 @@ | ||
| package g3001_3100.s3020_find_the_maximum_number_of_elements_in_subset; | ||
|
|
||
| // #Medium #Array #Hash_Table #Enumeration #2024_02_29_Time_51_ms_(94.80%)_Space_57_MB_(41.88%) | ||
|
|
||
| import java.util.HashMap; | ||
| import java.util.Map; | ||
|
|
||
| public class Solution { | ||
| public int maximumLength(int[] nums) { | ||
| return withHashMap(nums); | ||
| } | ||
|
|
||
| private int withHashMap(int[] nums) { | ||
| Map<Integer, Integer> map = new HashMap<>(); | ||
| for (int i : nums) { | ||
| map.put(i, map.getOrDefault(i, 0) + 1); | ||
| } | ||
| int ans = 0; | ||
| if (map.containsKey(1)) { | ||
| if (map.get(1) % 2 == 0) { | ||
| ans = map.get(1) - 1; | ||
| } else { | ||
| ans = map.get(1); | ||
| } | ||
| } | ||
| for (int key : map.keySet()) { | ||
| if (key == 1) { | ||
| continue; | ||
| } | ||
| int len = findSeries(map, key); | ||
| ans = Math.max(ans, len); | ||
| } | ||
| return ans; | ||
| } | ||
|
|
||
| private int findSeries(Map<Integer, Integer> map, int key) { | ||
| int sqr = key * key; | ||
| if (map.containsKey(sqr)) { | ||
| if (map.get(key) >= 2) { | ||
| return 2 + findSeries(map, sqr); | ||
| } else { | ||
| return 1; | ||
| } | ||
| } else { | ||
| return 1; | ||
| } | ||
| } | ||
| } |
32 changes: 32 additions & 0 deletions
32
...n/java/g3001_3100/s3020_find_the_maximum_number_of_elements_in_subset/readme.md
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,32 @@ | ||
| 3020\. Find the Maximum Number of Elements in Subset | ||
|
|
||
| Medium | ||
|
|
||
| You are given an array of **positive** integers `nums`. | ||
|
|
||
| You need to select a subset of `nums` which satisfies the following condition: | ||
|
|
||
| * You can place the selected elements in a **0-indexed** array such that it follows the pattern: <code>[x, x<sup>2</sup>, x<sup>4</sup>, ..., x<sup>k/2</sup>, x<sup>k</sup>, x<sup>k/2</sup>, ..., x<sup>4</sup>, x<sup>2</sup>, x]</code> (**Note** that `k` can be be any **non-negative** power of `2`). For example, `[2, 4, 16, 4, 2]` and `[3, 9, 3]` follow the pattern while `[2, 4, 8, 4, 2]` does not. | ||
|
|
||
| Return _the **maximum** number of elements in a subset that satisfies these conditions._ | ||
|
|
||
| **Example 1:** | ||
|
|
||
| **Input:** nums = [5,4,1,2,2] | ||
|
|
||
| **Output:** 3 | ||
|
|
||
| **Explanation:** We can select the subset {4,2,2}, which can be placed in the array as [2,4,2] which follows the pattern and 2<sup>2</sup> == 4. Hence the answer is 3. | ||
|
|
||
| **Example 2:** | ||
|
|
||
| **Input:** nums = [1,3,2,4] | ||
|
|
||
| **Output:** 1 | ||
|
|
||
| **Explanation:** We can select the subset {1}, which can be placed in the array as [1] which follows the pattern. Hence the answer is 1. Note that we could have also selected the subsets {2}, {3}, or {4}, there may be multiple subsets which provide the same answer. | ||
|
|
||
| **Constraints:** | ||
|
|
||
| * <code>2 <= nums.length <= 10<sup>5</sup></code> | ||
| * <code>1 <= nums[i] <= 10<sup>9</sup></code> |
11 changes: 11 additions & 0 deletions
11
src/main/java/g3001_3100/s3021_alice_and_bob_playing_flower_game/Solution.java
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,11 @@ | ||
| package g3001_3100.s3021_alice_and_bob_playing_flower_game; | ||
|
|
||
| // #Medium #Math #2024_02_29_Time_0_ms_(100.00%)_Space_40.8_MB_(25.85%) | ||
|
|
||
| public class Solution { | ||
| public long flowerGame(long n, long m) { | ||
| long ans = 0; | ||
| ans += ((n + 1) / 2) * (m / 2) + ((m + 1) / 2) * (n / 2); | ||
| return ans; | ||
| } | ||
| } |
39 changes: 39 additions & 0 deletions
39
src/main/java/g3001_3100/s3021_alice_and_bob_playing_flower_game/readme.md
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,39 @@ | ||
| 3021\. Alice and Bob Playing Flower Game | ||
|
|
||
| Medium | ||
|
|
||
| Alice and Bob are playing a turn-based game on a circular field surrounded by flowers. The circle represents the field, and there are `x` flowers in the clockwise direction between Alice and Bob, and `y` flowers in the anti-clockwise direction between them. | ||
|
|
||
| The game proceeds as follows: | ||
|
|
||
| 1. Alice takes the first turn. | ||
| 2. In each turn, a player must choose either the clockwise or anti-clockwise direction and pick one flower from that side. | ||
| 3. At the end of the turn, if there are no flowers left at all, the **current** player captures their opponent and wins the game. | ||
|
|
||
| Given two integers, `n` and `m`, the task is to compute the number of possible pairs `(x, y)` that satisfy the conditions: | ||
|
|
||
| * Alice must win the game according to the described rules. | ||
| * The number of flowers `x` in the clockwise direction must be in the range `[1,n]`. | ||
| * The number of flowers `y` in the anti-clockwise direction must be in the range `[1,m]`. | ||
|
|
||
| Return _the number of possible pairs_ `(x, y)` _that satisfy the conditions mentioned in the statement_. | ||
|
|
||
| **Example 1:** | ||
|
|
||
| **Input:** n = 3, m = 2 | ||
|
|
||
| **Output:** 3 | ||
|
|
||
| **Explanation:** The following pairs satisfy conditions described in the statement: (1,2), (3,2), (2,1). | ||
|
|
||
| **Example 2:** | ||
|
|
||
| **Input:** n = 1, m = 1 | ||
|
|
||
| **Output:** 0 | ||
|
|
||
| **Explanation:** No pairs satisfy the conditions described in the statement. | ||
|
|
||
| **Constraints:** | ||
|
|
||
| * <code>1 <= n, m <= 10<sup>5</sup></code> |
27 changes: 27 additions & 0 deletions
27
...in/java/g3001_3100/s3022_minimize_or_of_remaining_elements_using_operations/Solution.java
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,27 @@ | ||
| package g3001_3100.s3022_minimize_or_of_remaining_elements_using_operations; | ||
|
|
||
| // #Hard #Array #Greedy #Bit_Manipulation #2024_02_29_Time_43_ms_(78.48%)_Space_56.6_MB_(23.73%) | ||
|
|
||
| public class Solution { | ||
| public int minOrAfterOperations(int[] nums, int k) { | ||
| int ans = 0; | ||
| int mask = 0; | ||
| for (int j = 30; j >= 0; j--) { | ||
| mask = mask | (1 << j); | ||
| int consecutiveAnd = mask; | ||
| int mergeCount = 0; | ||
| for (int i : nums) { | ||
| consecutiveAnd = consecutiveAnd & i; | ||
| if ((consecutiveAnd | ans) != ans) { | ||
| mergeCount++; | ||
| } else { | ||
| consecutiveAnd = mask; | ||
| } | ||
| } | ||
| if (mergeCount > k) { | ||
| ans |= (1 << j); | ||
| } | ||
| } | ||
| return ans; | ||
| } | ||
| } |
53 changes: 53 additions & 0 deletions
53
...a/g3001_3100/s3022_minimize_or_of_remaining_elements_using_operations/readme.md
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,53 @@ | ||
| 3022\. Minimize OR of Remaining Elements Using Operations | ||
|
|
||
| Hard | ||
|
|
||
| You are given a **0-indexed** integer array `nums` and an integer `k`. | ||
|
|
||
| In one operation, you can pick any index `i` of `nums` such that `0 <= i < nums.length - 1` and replace `nums[i]` and `nums[i + 1]` with a single occurrence of `nums[i] & nums[i + 1]`, where `&` represents the bitwise `AND` operator. | ||
|
|
||
| Return _the **minimum** possible value of the bitwise_ `OR` _of the remaining elements of_ `nums` _after applying **at most**_ `k` _operations_. | ||
|
|
||
| **Example 1:** | ||
|
|
||
| **Input:** nums = [3,5,3,2,7], k = 2 | ||
|
|
||
| **Output:** 3 | ||
|
|
||
| **Explanation:** Let's do the following operations: | ||
| 1. Replace nums[0] and nums[1] with (nums[0] & nums[1]) so that nums becomes equal to [1,3,2,7]. | ||
| 2. Replace nums[2] and nums[3] with (nums[2] & nums[3]) so that nums becomes equal to [1,3,2]. | ||
|
|
||
| The bitwise-or of the final array is 3. | ||
|
|
||
| It can be shown that 3 is the minimum possible value of the bitwise OR of the remaining elements of nums after applying at most k operations. | ||
|
|
||
| **Example 2:** | ||
|
|
||
| **Input:** nums = [7,3,15,14,2,8], k = 4 | ||
|
|
||
| **Output:** 2 | ||
|
|
||
| **Explanation:** Let's do the following operations: | ||
| 1. Replace nums[0] and nums[1] with (nums[0] & nums[1]) so that nums becomes equal to [3,15,14,2,8]. | ||
| 2. Replace nums[0] and nums[1] with (nums[0] & nums[1]) so that nums becomes equal to [3,14,2,8]. | ||
| 3. Replace nums[0] and nums[1] with (nums[0] & nums[1]) so that nums becomes equal to [2,2,8]. | ||
| 4. Replace nums[1] and nums[2] with (nums[1] & nums[2]) so that nums becomes equal to [2,0]. | ||
|
|
||
| The bitwise-or of the final array is 2. | ||
|
|
||
| It can be shown that 2 is the minimum possible value of the bitwise OR of the remaining elements of nums after applying at most k operations. | ||
|
|
||
| **Example 3:** | ||
|
|
||
| **Input:** nums = [10,7,10,3,9,14,9,4], k = 1 | ||
|
|
||
| **Output:** 15 | ||
|
|
||
| **Explanation:** Without applying any operations, the bitwise-or of nums is 15. It can be shown that 15 is the minimum possible value of the bitwise OR of the remaining elements of nums after applying at most k operations. | ||
|
|
||
| **Constraints:** | ||
|
|
||
| * <code>1 <= nums.length <= 10<sup>5</sup></code> | ||
| * <code>0 <= nums[i] < 2<sup>30</sup></code> | ||
| * `0 <= k < nums.length` |
20 changes: 20 additions & 0 deletions
20
src/main/java/g3001_3100/s3024_type_of_triangle/Solution.java
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,20 @@ | ||
| package g3001_3100.s3024_type_of_triangle; | ||
|
|
||
| // #Easy #Array #Math #Sorting #2024_02_29_Time_0_ms_(100.00%)_Space_41.6_MB_(95.74%) | ||
|
|
||
| public class Solution { | ||
| public String triangleType(int[] nums) { | ||
| if (nums[0] + nums[1] > nums[2] | ||
| && nums[1] + nums[2] > nums[0] | ||
| && nums[2] + nums[0] > nums[1]) { | ||
| if (nums[0] == nums[1] && nums[1] == nums[2]) { | ||
| return "equilateral"; | ||
| } else if (nums[0] == nums[1] || nums[0] == nums[2] || nums[2] == nums[1]) { | ||
| return "isosceles"; | ||
| } else { | ||
| return "scalene"; | ||
| } | ||
| } | ||
| return "none"; | ||
| } | ||
| } |
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,42 @@ | ||
| 3024\. Type of Triangle | ||
|
|
||
| Easy | ||
|
|
||
| You are given a **0-indexed** integer array `nums` of size `3` which can form the sides of a triangle. | ||
|
|
||
| * A triangle is called **equilateral** if it has all sides of equal length. | ||
| * A triangle is called **isosceles** if it has exactly two sides of equal length. | ||
| * A triangle is called **scalene** if all its sides are of different lengths. | ||
|
|
||
| Return _a string representing_ _the type of triangle that can be formed_ _or_ `"none"` _if it **cannot** form a triangle._ | ||
|
|
||
| **Example 1:** | ||
|
|
||
| **Input:** nums = [3,3,3] | ||
|
|
||
| **Output:** "equilateral" | ||
|
|
||
| **Explanation:** Since all the sides are of equal length, therefore, it will form an equilateral triangle. | ||
|
|
||
| **Example 2:** | ||
|
|
||
| **Input:** nums = [3,4,5] | ||
|
|
||
| **Output:** "scalene" | ||
|
|
||
| **Explanation:** | ||
|
|
||
| nums[0] + nums[1] = 3 + 4 = 7, which is greater than nums[2] = 5. | ||
|
|
||
| nums[0] + nums[2] = 3 + 5 = 8, which is greater than nums[1] = 4. | ||
|
|
||
| nums[1] + nums[2] = 4 + 5 = 9, which is greater than nums[0] = 3. | ||
|
|
||
| Since the sum of the two sides is greater than the third side for all three cases, therefore, it can form a triangle. | ||
|
|
||
| As all the sides are of different lengths, it will form a scalene triangle. | ||
|
|
||
| **Constraints:** | ||
|
|
||
| * `nums.length == 3` | ||
| * `1 <= nums[i] <= 100` |
28 changes: 28 additions & 0 deletions
28
src/main/java/g3001_3100/s3025_find_the_number_of_ways_to_place_people_i/Solution.java
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,28 @@ | ||
| package g3001_3100.s3025_find_the_number_of_ways_to_place_people_i; | ||
|
|
||
| // #Medium #Array #Math #Sorting #Enumeration #Geometry | ||
| // #2024_02_29_Time_5_ms_(99.84%)_Space_44.7_MB_(30.13%) | ||
|
|
||
| import java.util.Arrays; | ||
|
|
||
| public class Solution { | ||
| public int numberOfPairs(int[][] points) { | ||
| Arrays.sort(points, (a, b) -> a[0] == b[0] ? b[1] - a[1] : a[0] - b[0]); | ||
| int cnt = 0; | ||
| for (int i = 0; i < points.length; i++) { | ||
| int bot = Integer.MIN_VALUE; | ||
| int top = points[i][1]; | ||
| for (int j = i + 1; j < points.length; j++) { | ||
| int y1 = points[j][1]; | ||
| if (y1 <= top && y1 > bot) { | ||
| cnt++; | ||
| bot = y1; | ||
| if (y1 == top) { | ||
| top--; | ||
| } | ||
| } | ||
| } | ||
| } | ||
| return cnt; | ||
| } | ||
| } |
69 changes: 69 additions & 0 deletions
69
src/main/java/g3001_3100/s3025_find_the_number_of_ways_to_place_people_i/readme.md
This file contains bidirectional Unicode text that may be interpreted or compiled differently than what appears below. To review, open the file in an editor that reveals hidden Unicode characters.
Learn more about bidirectional Unicode characters
| Original file line number | Diff line number | Diff line change |
|---|---|---|
| @@ -0,0 +1,69 @@ | ||
| 3025\. Find the Number of Ways to Place People I | ||
|
|
||
| Medium | ||
|
|
||
| You are given a 2D array `points` of size `n x 2` representing integer coordinates of some points on a 2D-plane, where <code>points[i] = [x<sub>i</sub>, y<sub>i</sub>]</code>. | ||
|
|
||
| We define the **right** direction as positive x-axis (**increasing x-coordinate**) and the **left** direction as negative x-axis (**decreasing x-coordinate**). Similarly, we define the **up** direction as positive y-axis (**increasing y-coordinate**) and the **down** direction as negative y-axis (**decreasing y-coordinate**) | ||
|
|
||
| You have to place `n` people, including Alice and Bob, at these points such that there is **exactly one** person at every point. Alice wants to be alone with Bob, so Alice will build a rectangular fence with Alice's position as the **upper left corner** and Bob's position as the **lower right corner** of the fence (**Note** that the fence **might not** enclose any area, i.e. it can be a line). If any person other than Alice and Bob is either **inside** the fence or **on** the fence, Alice will be sad. | ||
|
|
||
| Return _the number of **pairs of points** where you can place Alice and Bob, such that Alice **does not** become sad on building the fence_. | ||
|
|
||
| **Note** that Alice can only build a fence with Alice's position as the upper left corner, and Bob's position as the lower right corner. For example, Alice cannot build either of the fences in the picture below with four corners `(1, 1)`, `(1, 3)`, `(3, 1)`, and `(3, 3)`, because: | ||
|
|
||
| * With Alice at `(3, 3)` and Bob at `(1, 1)`, Alice's position is not the upper left corner and Bob's position is not the lower right corner of the fence. | ||
| * With Alice at `(1, 3)` and Bob at `(1, 1)`, Bob's position is not the lower right corner of the fence. | ||
|
|
||
| 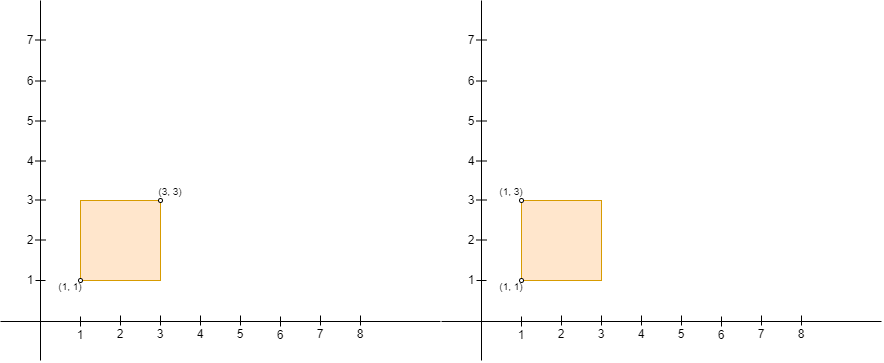 | ||
|
|
||
| **Example 1:** | ||
|
|
||
| 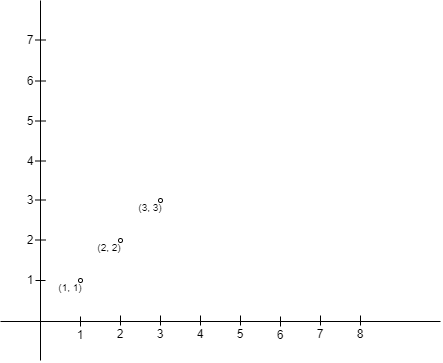 | ||
|
|
||
| **Input:** points = [[1,1],[2,2],[3,3]] | ||
|
|
||
| **Output:** 0 | ||
|
|
||
| **Explanation:** There is no way to place Alice and Bob such that Alice can build a fence with Alice's position as the upper left corner and Bob's position as the lower right corner. Hence we return 0. | ||
|
|
||
| **Example 2:** | ||
|
|
||
| 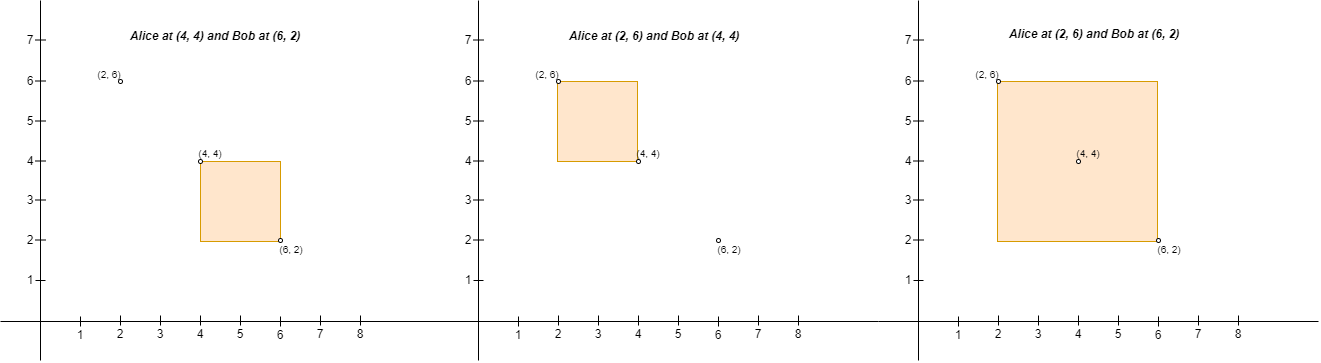 | ||
|
|
||
| **Input:** points = [[6,2],[4,4],[2,6]] | ||
|
|
||
| **Output:** 2 | ||
|
|
||
| **Explanation:** There are two ways to place Alice and Bob such that Alice will not be sad: | ||
|
|
||
| - Place Alice at (4, 4) and Bob at (6, 2). | ||
|
|
||
| - Place Alice at (2, 6) and Bob at (4, 4). | ||
|
|
||
| You cannot place Alice at (2, 6) and Bob at (6, 2) because the person at (4, 4) will be inside the fence. | ||
|
|
||
| **Example 3:** | ||
|
|
||
| 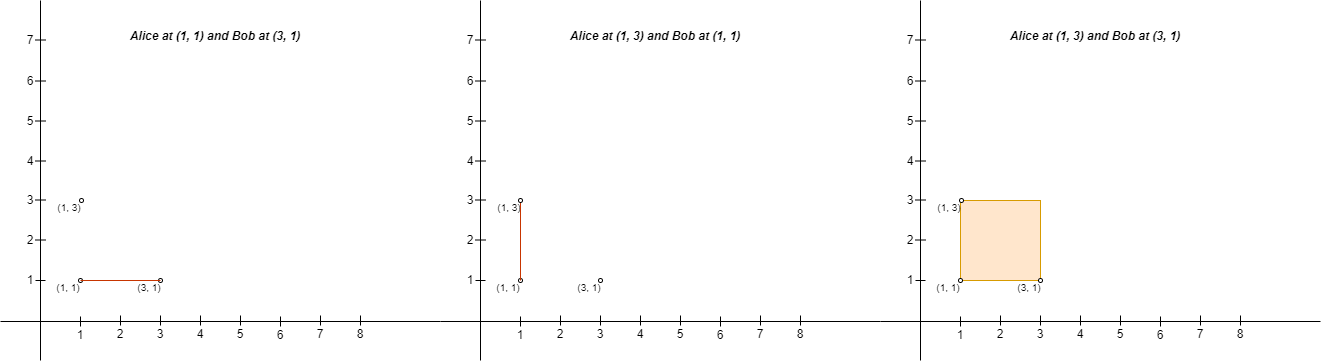 | ||
|
|
||
| **Input:** points = [[3,1],[1,3],[1,1]] | ||
|
|
||
| **Output:** 2 | ||
|
|
||
| **Explanation:** There are two ways to place Alice and Bob such that Alice will not be sad: | ||
|
|
||
| - Place Alice at (1, 1) and Bob at (3, 1). | ||
|
|
||
| - Place Alice at (1, 3) and Bob at (1, 1). | ||
|
|
||
| You cannot place Alice at (1, 3) and Bob at (3, 1) because the person at (1, 1) will be on the fence. | ||
|
|
||
| Note that it does not matter if the fence encloses any area, the first and second fences in the image are valid. | ||
|
|
||
| **Constraints:** | ||
|
|
||
| * `2 <= n <= 50` | ||
| * `points[i].length == 2` | ||
| * `0 <= points[i][0], points[i][1] <= 50` | ||
| * All `points[i]` are distinct. |
Oops, something went wrong.