-
Notifications
You must be signed in to change notification settings - Fork 334
mesh
In addition to support of exact geometrical representation of 3D objects Open CASCADE Technology provides functionality to work with tessellated representations of objects in form of meshes.
Open CASCADE Technology mesh functionality provides:
- data structures to store surface mesh data associated to shapes, and some basic algorithms to handle these data
- data structures and algorithms to build surface triangular mesh from BRep objects (shapes).
- tools to extend 3D visualization capabilities of Open CASCADE Technology with displaying meshes along with associated pre- and post-processor data.
Open CASCADE Technology includes two mesh converters:
- VRML converter translates Open CASCADE shapes to VRML 1.0 files (Virtual Reality Modeling Language). Open CASCADE shapes may be translated in two representations: shaded or wireframe. A shaded representation present shapes as sets of triangles computed by a mesh algorithm while a wireframe representation present shapes as sets of curves.
- STL converter translates Open CASCADE shapes to STL files. STL (STtereoLithography) format is widely used for rapid prototyping.
Open CASCADE SAS also offers Advanced Mesh Products:
Besides, we can efficiently help you in the fields of surface and volume meshing algorithms, mesh optimization algorithms etc. If you require a qualified advice about meshing algorithms, do not hesitate to benefit from the expertise of our team in that domain.
The projects dealing with numerical simulation can benefit from using SALOME - an Open Source Framework for CAE with CAD data interfaces, generic Pre- and Post- F.E. processors and API for integrating F.E. solvers.
Learn more about SALOME platform on https://www.salome-platform.org
The algorithm of shape triangulation is provided by the functionality of BRepMesh_IncrementalMesh class, which adds a triangulation of the shape to its topological data structure. This triangulation is used to visualize the shape in shaded mode.
#include <IMeshData_Status.hxx>
#include <IMeshTools_Parameters.hxx>
#include <BRepMesh_IncrementalMesh.hxx>
Standard_Boolean meshing_explicit_parameters()
{
const Standard_Real aRadius = 10.0;
const Standard_Real aHeight = 25.0;
BRepPrimAPI_MakeCylinder aCylinder(aRadius, aHeight);
TopoDS_Shape aShape = aCylinder.Shape();
const Standard_Real aLinearDeflection = 0.01;
const Standard_Real anAngularDeflection = 0.5;
BRepMesh_IncrementalMesh aMesher (aShape, aLinearDeflection, Standard_False, anAngularDeflection, Standard_True);
const Standard_Integer aStatus = aMesher.GetStatusFlags();
return !aStatus;
}
Standard_Boolean meshing_imeshtools_parameters()
{
const Standard_Real aRadius = 10.0;
const Standard_Real aHeight = 25.0;
BRepPrimAPI_MakeCylinder aCylinder(aRadius, aHeight);
TopoDS_Shape aShape = aCylinder.Shape();
IMeshTools_Parameters aMeshParams;
aMeshParams.Deflection = 0.01;
aMeshParams.Angle = 0.5;
aMeshParams.Relative = Standard_False;
aMeshParams.InParallel = Standard_True;
aMeshParams.MinSize = Precision::Confusion();
aMeshParams.InternalVerticesMode = Standard_True;
aMeshParams.ControlSurfaceDeflection = Standard_True;
BRepMesh_IncrementalMesh aMesher (aShape, aMeshParams);
const Standard_Integer aStatus = aMesher.GetStatusFlags();
return !aStatus;
}
The default meshing algorithm BRepMesh_IncrementalMesh has two major options to define triangulation -- linear and angular deflections.
At the first step all edges from a face are discretized according to the specified parameters.
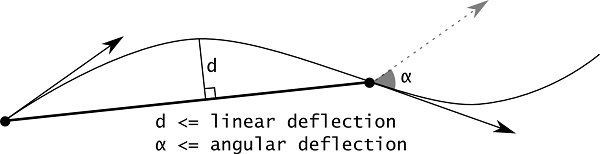
At the second step, the faces are tessellated. Linear deflection limits the distance between a curve and its tessellation, whereas angular deflection limits the angle between subsequent segments in a polyline.
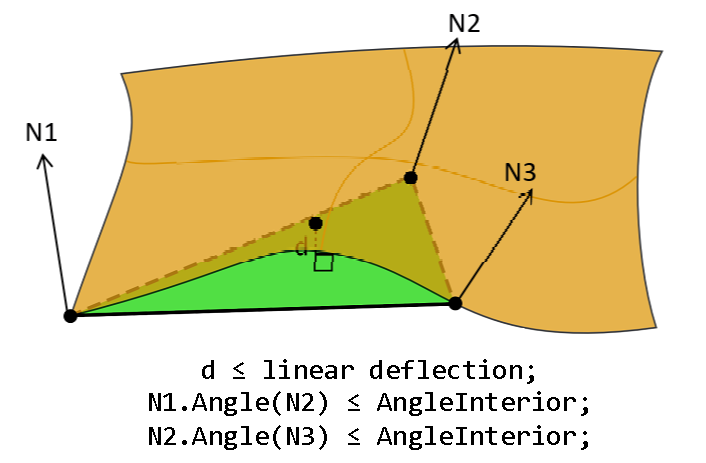
There are additional options to control behavior of the meshing of face interior: DeflectionInterior and AngleInterior. DeflectionInterior limits the distance between triangles and the face interior. AngleInterior (used for tessellation of B-spline faces only) limits the angle between normals (N1, N2 and N3 in the picture) in the nodes of every link of the triangle. There is an exception for the links along the face boundary edges, "Angular Deflection" is used for them during edges discretization.
Note that if a given value of linear deflection is less than shape tolerance then the algorithm will skip this value and will take into account the shape tolerance.
The application should provide deflection parameters to compute a satisfactory mesh. Angular deflection is relatively simple and allows using a default value (12-20 degrees). Linear deflection has an absolute meaning and the application should provide the correct value for its models. Giving small values may result in a too huge mesh (consuming a lot of memory, which results in a long computation time and slow rendering) while big values result in an ugly mesh.
For an application working in dimensions known in advance it can be reasonable to use the absolute linear deflection for all models. This provides meshes according to metrics and precision used in the application (for example, it it is known that the model will be stored in meters, 0.004 m is enough for most tasks).
However, an application that imports models created in other applications may not use the same deflection for all models. Note that actually this is an abnormal situation and this application is probably just a viewer for CAD models with dimensions varying by an order of magnitude. This problem can be solved by introducing the concept of a relative linear deflection with some LOD (level of detail). The level of detail is a scale factor for absolute deflection, which is applied to model dimensions.
Meshing covers a shape with a triangular mesh. Other than hidden line removal, you can use meshing to transfer the shape to another tool: a manufacturing tool, a shading algorithm, a finite element algorithm, or a collision algorithm.
You can obtain information on the shape by first exploring it. To access triangulation of a face in the shape later, use BRepTool::Triangulation. To access a polygon, which is the approximation of an edge of the face, use BRepTool::PolygonOnTriangulation.
The main goals of the chosen architecture are:
- Remove tight connections between data structures, auxiliary tools and algorithms to create an extensible solution, easy for maintenance and improvements;
- Separate the code among several functional units responsible for specific operation for the sake of simplification of debugging and readability;
- Introduce new data structures enabling the possibility to manipulate a discrete model of a particular entity (edge, wire, face) in order to perform computations locally instead of processing the entire model;
- Implement a new triangulation algorithm replacing the existing functionality that contains overcomplicated solutions that need to be moved to the upper level. In addition, provide the possibility to change the algorithm depending on surface type (initially to speed up meshing of planes).
Generally, the workflow of the component can be divided into six parts:
- Creation of model data structure: source TopoDS_Shape passed to algorithm is analyzed and exploded into faces and edges. The reflection corresponding to each topological entity is created in the data model. Note that underlying algorithms use the data model as input and access it via a common interface which allows creating a custom data model with necessary dependencies between particular entities (see the paragraph "Data model interface");
- Discretize edges 3D & 2D curves: 3D curve as well as an associated set of 2D curves of each model edge is discretized in order to create a coherent skeleton used as a base in face meshing process. If an edge of the source shape already contains polygonal data which suits the specified parameters, it is extracted from the shape and stored in the model as is. Each edge is processed separately, the adjacency is not taken into account;
- Heal discrete model: the source TopoDS_Shape can contain problems, such as open wires or self-intersections, introduced during design, exchange or modification of model. In addition, some problems like self-intersections can be introduced by roughly discretized edges. This stage is responsible for analysis of a discrete model in order to detect and repair problems or to refuse further processing of a model part in case if a problem cannot be solved;
- Preprocess discrete model: defines actions specific to the implemented approach to be performed before meshing of faces. By default, this operation iterates over model faces, checks the consistency of existing triangulations and cleans topological faces and adjacent edges from polygonal data in case of inconsistency or marks a face of the discrete model as not required for the computation;
- Discretize faces: represents the core part performing mesh generation for a particular face based on 2D discrete data. This operation caches polygonal data associated with face edges in the data model for further processing and stores the generated mesh to TopoDS_Face;
- Postprocess discrete model: defines actions specific for the implemented approach to be performed after meshing of faces. By default, this operation stores polygonal data obtained at the previous stage to TopoDS_Edge objects of the source model.
The component structure contains two units: IMeshData (see Data model interface) and IMeshTools, defining common interfaces for the data model and algorithmic tools correspondingly. Class IMeshTools_Context represents a connector between these units. The context class caches the data model as well as the tools corresponding to each of six stages of the workflow mentioned above and provides methods to call the corresponding tool safely (designed similarly to IntTools_Context in order to keep consistency with OCCT core tools). All stages, except for the first one, use the data model as input and perform a specific action on the entire structure. Thus, API class IMeshTools_ModelAlgo is defined in order to unify the interface of tools manipulating the data model. Each tool supposed to process the data model should inherit this interface enabling the possibility to cache it in context. In contrast to others, the model builder interface is defined by another class IMeshTools_ModelBuilder due to a different meaning of the stage. The entry point starting the entire workflow is represented by IMeshTools_MeshBuilder.
The default implementation of IMeshTools_Context is given in BRepMesh_Context class initializing the context by instances of default algorithmic tools.
The factory interface IMeshTools_MeshAlgoFactory gives the possibility to change the triangulation algorithm for a specific surface. The factory returns an instance of the triangulation algorithm via IMeshTools_MeshAlgo interface depending on the type of surface passed as parameter. It is supposed to be used at the face discretization stage.
The default implementation of AlgoFactory is given in BRepMesh_MeshAlgoFactory returning algorithms of different complexity chosen according to the passed surface type. In its turn, it is used as the initializer of BRepMesh_FaceDiscret algorithm representing the starter of face discretization stage.
Remaining interfaces describe auxiliary tools:
- IMeshTools_CurveTessellator: provides a common interface to the algorithms responsible for creation of discrete polygons on 3D and 2D curves as well as tools for extraction of existing polygons from TopoDS_Edge allowing to obtain discrete points and the corresponding parameters on curve regardless of the implementation details (see examples of usage of derived classes BRepMesh_CurveTessellator, BRepMesh_EdgeTessellationExtractor in BRepMesh_EdgeDiscret);
- IMeshTools_ShapeExplorer: the last two interfaces represent visitor design pattern and are intended to separate iteration over elements of topological shape (edges and faces) from the operations performed on a particular element;
- IMeshTools_ShapeVisitor: provides a common interface for operations on edges and faces of the target topological shape. It can be used in couple with IMeshTools_ShapeExplorer. The default implementation available in BRepMesh_ShapeVisitor performs initialization of the data model. The advantage of such approach is that the implementation of IMeshTools_ShapeVisitor can be changed according to the specific data model whereas the shape explorer implementation remains the same.
The data structures intended to keep discrete and temporary data required by underlying algorithms are created at the first stage of the meshing procedure. Generally, the model represents dependencies between entities of the source topological shape suitable for the target task.
Unit IMeshData provides common interfaces specifying the data model API used on different stages of the entire workflow. Dependencies and references of the designed interfaces are given in the figure below. A specific interface implementation depends on the target application which allows the developer to implement different models and use custom low-level data structures, e.g. different collections, either NCollection or STL. IMeshData_Shape is used as the base class for all data structures and tools keeping the topological shape in order to avoid possible copy-paste.
The default implementation of interfaces is given in BRepMeshData unit. The main aim of the default data model is to provide features performing discretization of edges in a parallel mode. Thus, curve, pcurve and other classes are based on STL containers and smart-pointers as far as NCollection does not provide thread-safety for some cases (e.g. NCollection_Sequence). In addition, it closely reflects topology of the source shape, i.e. the number of edges in the data model is equal to the number of edges in the source model; each edge contains a set of pcurves associated with its adjacent faces which allows creation of discrete polygons for all pcurves or the 3D curve of a particular edge in a separate thread.
Advantages: In case of necessity, the data model (probably with algorithms for its processing) can be easily substituted by another implementation supporting another kind of dependencies between elements.
An additional example of a different data model is the case when it is not required to create a mesh with discrete polygons synchronized between adjacent faces, i.e. in case of necessity to speed up creation of a rough per-face tessellation used for visualization or quick computation only (the approach used in XDEDRAW_Props).
At this stage the data model is filled by entities according to the topological structure of the source shape. A default implementation of the data model is given in BRepMeshData unit and represents the model as two sets: a set of edges and a set of faces. Each face consists of one or several wires, the first of which always represents the outer wire, while others are internal. In its turn, each wire depicts the ordered sequence of oriented edges. Each edge is characterized by a single 3D curve and zero (in case of free edge) or more 2D curves associated with faces adjacent to this edge. Both 3D and 2D curves represent a set of pairs point-parameter defined in 3D and 2D space of the reference face correspondingly. An additional difference between a curve and a pcurve is that the latter has a reference to the face it is defined for.
Model filler algorithm is represented by BRepMesh_ShapeVisitor class creating the model as a reflection to topological shape with help of BRepMesh_ShapeExplorer performing iteration over edges and faces of the target shape. Note that the algorithm operates on a common interface of the data model and creates a structure without any knowledge about the implementation details and underlying data structures. The entry point to collecting functionality is BRepMesh_ModelBuilder class.
At this stage only the edges of the data model are considered. Each edge is processed separately (with the possibility to run processing in multiple threads). The edge is checked for existing polygonal data. In case if at least one representation exists and suits the meshing parameters, it is recuperated and used as reference data for tessellation of the whole set of pcurves as well as 3D curve assigned to the edge (see BRepMesh_EdgeTessellationExtractor). Otherwise, a new tessellation algorithm is created and used to generate the initial polygon (see BRepMesh_CurveTessellator) and the edge is marked as outdated. In addition, the model edge is updated by deflection as well as recomputed same range, same parameter and degeneracy parameters. See BRepMesh_EdgeDiscret for implementation details.
IMeshData unit defines interface IMeshData_ParametersListArrayAdaptor, which is intended to adapt arbitrary data structures to the NCollection_Array1 container API. This solution is made to use both NCollection_Array1 and IMeshData_Curve as the source for BRepMesh_EdgeParameterProvider tool intended to generate a consistent parametrization taking into account the same parameter property.
In general, this stage represents a set of operations performed on the entire discrete model in order to resolve inconsistencies due to the problems caused by design, translation or rough discretization. A different sequence of operations can be performed depending on the target triangulation algorithm, e.g. there are different approaches to process self-intersections – either to amplify edges discretization by decreasing the target precision or to split links at the intersection points. At this stage the whole set of edges is considered in aggregate and their adjacency is taken into account. A default implementation of the model healer is given in BRepMesh_ModelHealer which performs the following actions:
- Iterates over model faces and checks their wires for consistency, i.e. whether the wires are closed and do not contain self-intersections. The data structures are designed free of collisions, thus it is possible to run processing in a parallel mode;
- Forcibly connects the ends of adjacent edges in the parametric space, closing gaps between possible disconnected parts. The aim of this operation is to create a correct discrete model defined relatively to the parametric space of the target face taking into account connectivity and tolerances of 3D space only. This means that no specific computations are made to determine U and V tolerance;
- Registers intersections on edges forming the face shape. Two solutions are possible in order to resolve self-intersection:
- Decrease deflection of a particular edge and update its discrete model. After that the workflow "intersection check – amplification" is repeated up to 5 times. As the result, target edges contain a finer tessellation and meshing continues or the face is marked by IMeshData_SelfIntersectingWire status and refused from further processing;
- Split target edges by intersection point and synchronize the updated polygon with curve and remaining pcurves associated to each edge. This operation presents a more robust solution comparing to the amplification procedure with a guaranteed result, but it is more difficult for implementation from the point of view of synchronization functionality.
This stage implements actions to be performed before meshing of faces. Depending on target goals it can be changed or omitted. By default, BRepMesh_ModelPreProcessor implements the functionality checking topological faces for consistency of existing triangulation, i.e.: consistency with the target deflection parameter; indices of nodes referenced by triangles do not exceed the number of nodes stored in a triangulation. If the face fails some checks, it is cleaned from triangulation and its adjacent edges are cleaned from existing polygons. This does not affect a discrete model and does not require any recomputation as the model keeps tessellations for the whole set of edges despite consistency of their polygons.
Discretization of faces is the general part of meshing algorithm. At this stage edges tessellation data obtained and processed on previous steps is used to form contours of target faces and passed as input to the triangulation algorithm. Default implementation is provided by BRepMesh_FaceDiscret class which represents a starter for triangulation algorithm. It iterates over faces available in the data model, creates an instance of the triangulation algorithm according to the type of surface associated with each face via IMeshTools_MeshAlgoFactory and executes it. Each face is processed separately, thus it is possible to process faces in a parallel mode. The class diagram of face discretization is given in the figure below.
In general, face meshing algorithms have the following structure:
- BRepMesh_BaseMeshAlgo implements IMeshTools_MeshAlgo interface and the base functionality for inherited algorithms. The main goal of this class is to initialize an instance of BRepMesh_DataStructureOfDelaun as well as auxiliary data structures suitable for nested algorithms using face model data passed as input parameter. Despite implementation of triangulation algorithm this structure is currently supposed as common for OCCT. However, the user is free to implement a custom algorithm and supporting data structure accessible via IMeshTools_MeshAlgo interface, e.g. to connect a 3-rd party meshing tool that does not support TopoDS_Shape out of box. For this, such structure provides the possibility to distribute connectors to various algorithms in the form of plugins;
- BRepMesh_DelaunayBaseMeshAlgo and BRepMesh_SweepLineMeshAlgo classes implement core meshing functionality operating directly on an instance of BRepMesh_DataStructureOfDelaun. The algorithms represent mesh generation tools adding new points from the data structure to the final mesh;
- BRepMesh_NodeInsertionMeshAlgo class represents a wrapper intended to extend the algorithm inherited from BRepMesh_BaseMeshAlgo to enable the functionality generating surface nodes and inserting them into the structure. On this level, an instance of the classification tool is created and can be used to accept-reject internal nodes. In addition, computations necessary for scaling UV coordinates of points relatively to the range specified for the corresponding direction are performed. As far as both triangulation algorithms work on static data provided by the structure, new nodes are added at the initialization stage. Surface nodes are generated by an auxiliary tool called range splitter and passed as template parameter (see Range splitter);
- Classes BRepMesh_DelaunayNodeInsertionMeshAlgo and BRepMesh_SweepLineNodeInsertionMeshAlgo implement algorithm-specific functionality related to addition of internal nodes supplementing functionality provided by BRepMesh_NodeInsertionMeshAlgo;
- BRepMesh_DelaunayDeflectionControlMeshAlgo extends functionality of BRepMesh_DelaunayNodeInsertionMeshAlgo by additional procedure controlling deflection of generated triangles.
BRepMesh provides user a way to switch default triangulation algorithm to a custom one, either implemented by user or available worldwide. There are three base classes that can be currently used to integrate 3rd-party algorithms:
- BRepMesh_ConstrainedBaseMeshAlgo base class for tools providing generation of triangulations with constraints requiring no common processing by BRepMesh;
- BRepMesh_CustomBaseMeshAlgo provides the entry point for generic algorithms without support of constraints and supposed for generation of base mesh only. Constraint edges are processed using standard functionality provided by the component itself upon background mesh produced by 3rd-party solver;
- BRepMesh_CustomDelaunayBaseMeshAlgo contains initialization part for tools used by BRepMesh for checks or optimizations using results of 3rd-party algorithm.
Meshing algorithms could be provided by implementing IMeshTools_MeshAlgoFactory with related interfaces and passing it to BRepMesh_Context::SetFaceDiscret(). OCCT comes with two base 2D meshing algorithms: BRepMesh_MeshAlgoFactory (used by default) and BRepMesh_DelabellaMeshAlgoFactory.
The following example demonstrates how it could be done from Draw environment:
psphere s 10
### Default Algo ###
incmesh s 0.0001 -algo default
### Delabella Algo ###
incmesh s 0.0001 -algo delabella
The code snippet below shows passing a custom mesh factory to BRepMesh_IncrementalMesh:
IMeshTools_Parameters aMeshParams;
Handle(IMeshTools_Context) aContext = new BRepMesh_Context();
aContext->SetFaceDiscret (new BRepMesh_FaceDiscret (new BRepMesh_DelabellaMeshAlgoFactory()));
BRepMesh_IncrementalMesh aMesher;
aMesher.SetShape (aShape);
aMesher.ChangeParameters() = aMeshParams;
aMesher.Perform (aContext);
Range splitter tools provide functionality to generate internal surface nodes defined within the range computed using discrete model data. The base functionality is provided by BRepMesh_DefaultRangeSplitter which can be used without modifications in case of planar surface. The default splitter does not generate any internal node.
BRepMesh_ConeRangeSplitter, BRepMesh_CylinderRangeSplitter and BRepMesh_SphereRangeSplitter are specializations of the default splitter intended for quick generation of internal nodes for the corresponding type of analytical surface.
BRepMesh_UVParamRangeSplitter implements base functionality taking discretization points of face border into account for node generation. Its successors BRepMesh_TorusRangeSplitter and BRepMesh_NURBSRangeSplitter extend the base functionality for toroidal and NURBS surfaces correspondingly.
This stage implements actions to be performed after meshing of faces. Depending on target goals it can be changed or omitted. By default, BRepMesh_ModelPostProcessor commits polygonal data stored in the data model to TopoDS_Edge.
© 2024 Open CASCADE Technology. All rights reserved.